 series expansions and answers" />
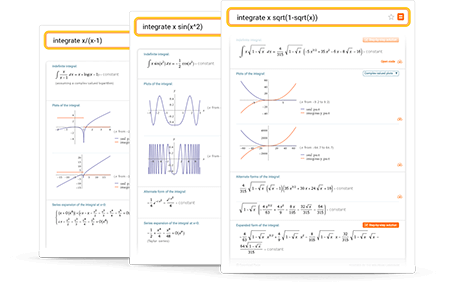
series expansions and answers" />Wolfram|Alpha является замечательным инструментом для нахождения первообразных и вычисления определенных интегралов, двойных или тройных интегралов, а также несобственных интегралов. Более того, она строит графики, предлагает альтернативные формы ответов, а также другую полезную информацию для развития вашей математической интуиции.
 series expansions and answers" />
series expansions and answers" />
Вводите запросы на обычном английском языке. Использование скобок, в случае необходимости, позволяет избежать неоднозначностей в запросе. Вот некоторые примеры, иллюстрирующие запросы для вычисления интеграла.
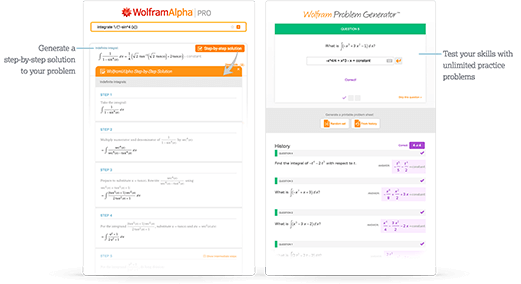
Get immediate feedback and guidance with step-by-step solutions for integrals and Wolfram Problem Generator
Неопределенный интеграл функции f(x), обозначаемый ∫f(x) dx, определяется как первообразная от f(x). Другими словами, производная от ∫f(x) dx равняется f(x). Поскольку производная от постоянной равна нулю, неопределенные интегралы определены с точностью до произвольной постоянной. Например, ∫sin(x) dx=−cos(x)+постоянная, потому что производная от −cos(x)+постоянная равняется sin(x). Определенный интеграл функции f(x) на отрезке от x=a до x=b, обозначаемый ∫baf(x) dx, определяется как суммарная площадь со знаком между кривой f(x) и осью абсцисс на отрезке от x=a до x=b.
Оба типа интегралов связаны друг с другом основной теоремой анализа. Она утверждает, что если функция f(x) является интегрируемой на отрезке [a,b] а F(x) является ее непрерывной первообразной, то ∫baf(x) dx=F(b)−F(a). Таким образом, ∫π0sin(x) dx=(−cos(π))−(−cos(0))=2. Иногда необходимо найти приближенное значение определенного интеграла. Распространенным методом вычисления приближения является размещение тонких прямоугольников под графиком функции и суммирование их площадей со знаком. Wolfram|Alpha может вычислять значения для широкого ряда интегралов.
Wolfram|Alpha находит значения не таким образом, как это делают люди. Она использует команду Integrate системы Mathematica, которая является результатом огромного объема математической и вычислительной научно-исследовательской работы. Команда Integrate вычисляет интегралы не так, как человек. Она использует эффективные и общие алгоритмы, часто включающие в себя сложные математические вычисления. Наиболее часто это происходит одним из двух способов. В первом - интеграл вычисляют в общем виде с неопределенными коэффициентами, результат дифференцируют и решают уравнения для этих коэффициентов так, чтобы получалось конкретное подынтегральное выражение. Даже для достаточно простых интегралов, генерируемые уравнения могут быть очень громоздкими, а для их решения могут требоваться сильные возможности системы Mathematica в алгебраических вычислениях. Другой подход, используемый системой Mathematica для вычисления интегралов, состоит в записи подынтегрального выражения в терминах обобщенных гипергеометрических функций и использовании ряда тождеств между функциями из этого весьма общего класса математических функций.
Несмотря на то, что эти эффективные алгоритмы дают Wolfram|Alpha возможность быстро находить значения интегралов и позволяют ей работать с широким рядом специальных функций, для неё также важно уметь вычислять интегралы так, как это делал бы человек. Поэтому Wolfram|Alpha имеет алгоритмы пошагового интегрирования. Они используют совершенно другую технику интегрирования, имитирующую способ решения интегралов, предпринимаемый людьми. Сюда входит интегрирование методом подстановки, интегрирование по частям, использование тригонометрических подстановок и метод Остроградского.